 外接球问题方法总结
外接球问题方法总结
582x479 - 229KB - PNG
秒杀立体几何外接球问题的几大方法
458x533 - 58KB - JPEG
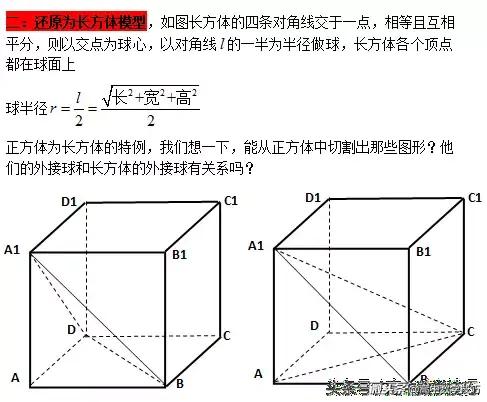 秒杀立体几何外接球问题的几大方法,识货的 - 今日头条(www.toutiao.com)
秒杀立体几何外接球问题的几大方法,识货的 - 今日头条(www.toutiao.com)
487x402 - 39KB - JPEG
秒杀立体几何外接球问题的几大方法,识货的赶快收藏
454x355 - 43KB - JPEG
秒杀立体几何外接球问题的几大方法
482x406 - 32KB - JPEG
 多面体的外接球问题
多面体的外接球问题
1080x810 - 77KB - JPEG
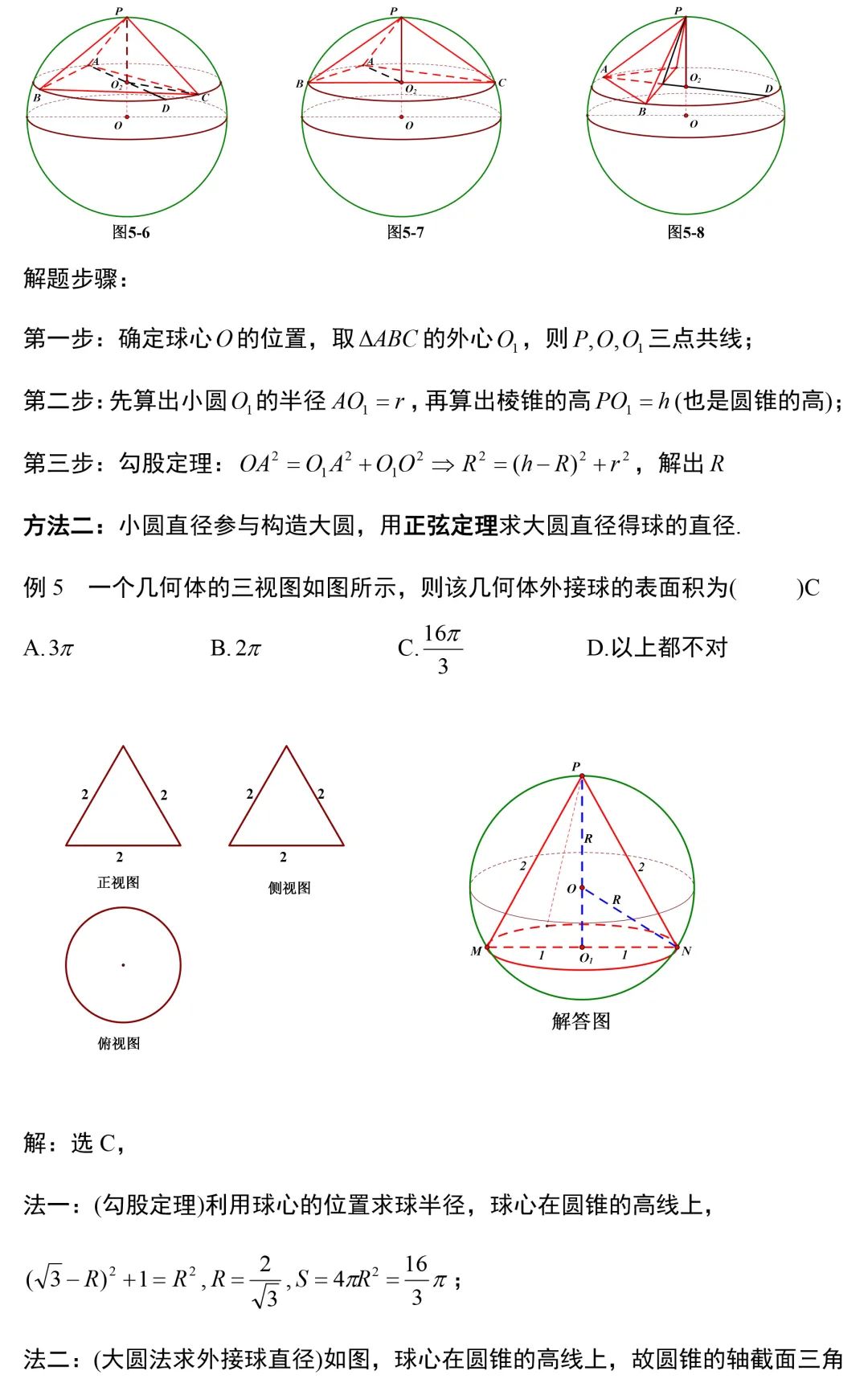 外接球与内切球解题方法,搞定这8大模型几何问题不用愁
外接球与内切球解题方法,搞定这8大模型几何问题不用愁
1080x1716 - 167KB - JPEG
 外接球与内切球解题方法,搞定这8大模型几何问题不用愁
外接球与内切球解题方法,搞定这8大模型几何问题不用愁
1080x1689 - 160KB - JPEG
 外接球与内切球解题方法,搞定这8大模型几何问题不用愁
外接球与内切球解题方法,搞定这8大模型几何问题不用愁
1080x1706 - 177KB - JPEG
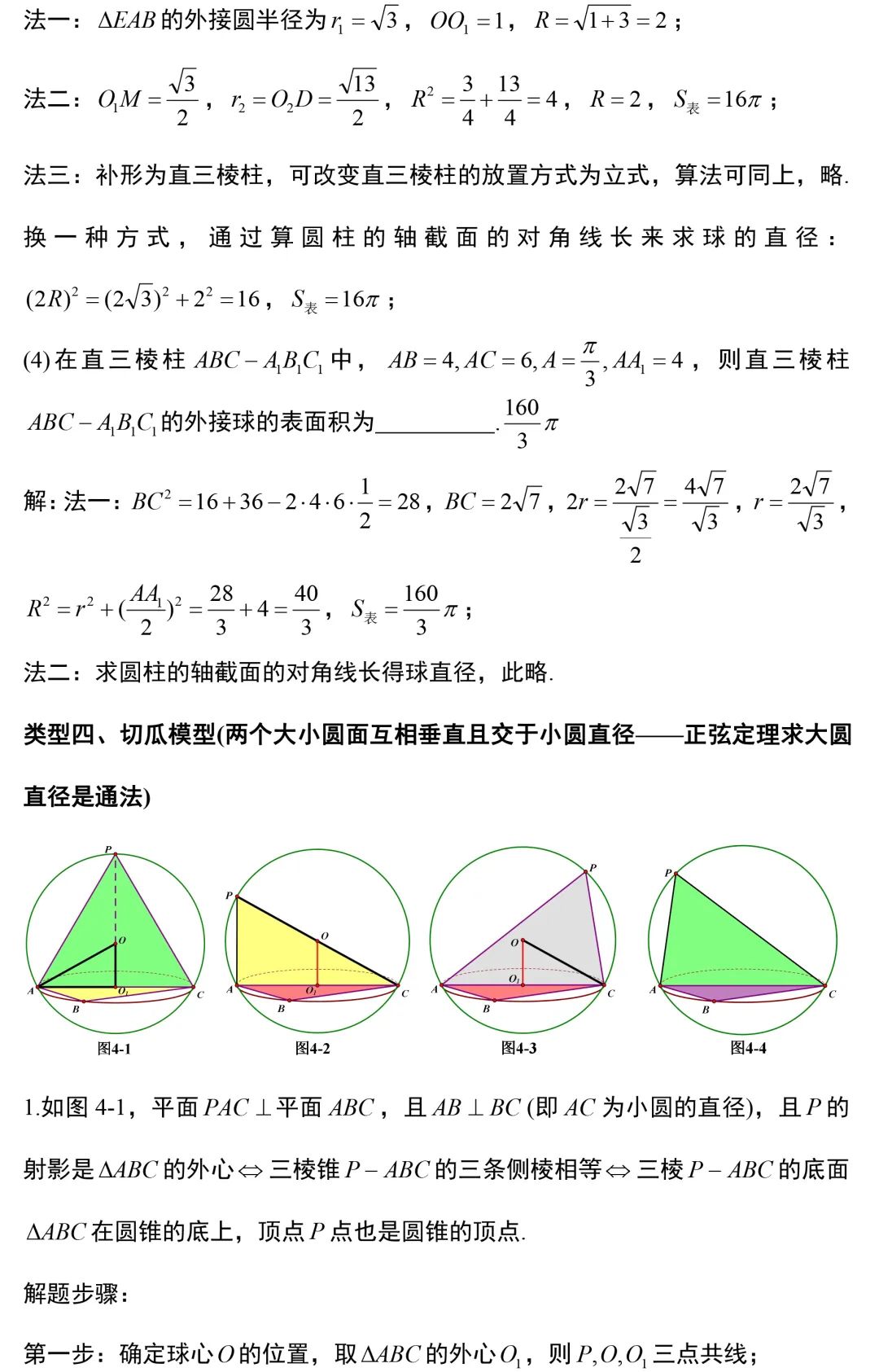 外接球与内切球解题方法,搞定这8大模型几何问题不用愁
外接球与内切球解题方法,搞定这8大模型几何问题不用愁
1080x1685 - 196KB - JPEG
 高中数学丨外接球与内切球解题方法,搞定
高中数学丨外接球与内切球解题方法,搞定
1080x1608 - 172KB - JPEG
 的位置关系与球 考点二 球的内切外接问题
的位置关系与球 考点二 球的内切外接问题
1058x1497 - 135KB - JPEG
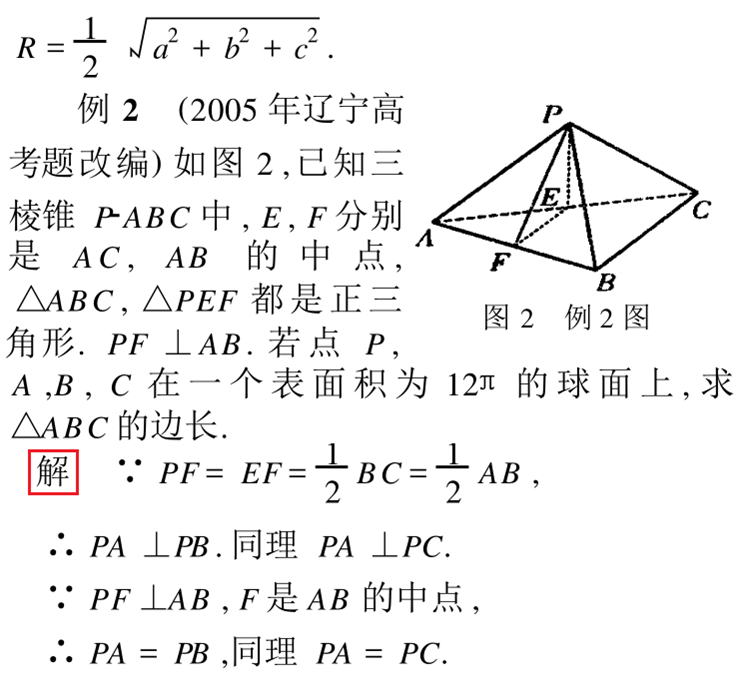 常见的四面体外接球问题.高中数学辅导
常见的四面体外接球问题.高中数学辅导
747x678 - 110KB - PNG
 巧解几何体的外接球问题
巧解几何体的外接球问题
1536x2012 - 991KB - PNG
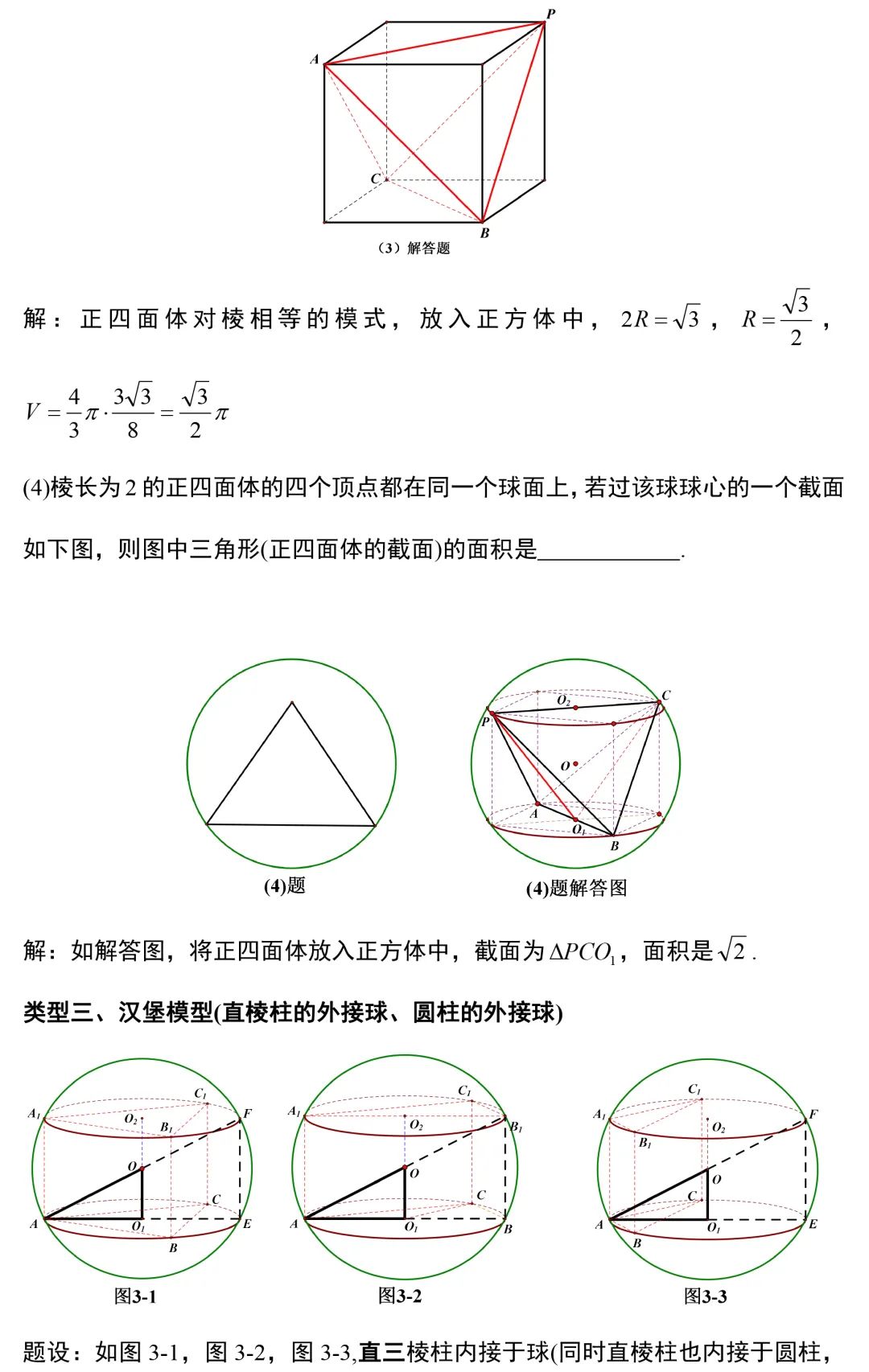 外接球与内切球解题方法,搞定这8大模型
外接球与内切球解题方法,搞定这8大模型
1080x1706 - 163KB - JPEG
外接球问题 李123419666|2020-03-10 VIP专享文档 VIP专享文档是百度文库认证用户/机构上传的专业性文档,文库VIP用户或购买VIP专享文档下载特权礼包的其他会员用户可
外接球问题典型例题 landy990261|2020-04-07 高考数学外接球 VIP专享文档 VIP专享文档是百度文库认证用户/机构上传的专业性文档,文库VIP用户或购买VIP专享文档下载特权
共享文档是百度文库用户免费上传的可与其他用户免费共享的文档,具体共享方式由上传人自由设定。只要带有以下“共享文档”标识的文档便是该类文档。了解文档类型 还剩
立体几何多面体与外接球问题专项归纳1、一个四棱柱的底面是正方形,侧棱与底面垂直,其长度为4,棱柱的体积为16,棱柱的各顶点在一个球面上,则这个球的表面积是( )A.16π B.20π C.24π D.32π2、一个正四面体的所有棱长都为,四个顶点在同一个球面上,则此球的表面积为( )A.3π B.4π C.3π D.6π3.在半球内有一个内接
[最佳答案] 之后通过圆的方程解出底面外心的为位置,然后连接外心和顶点,再用球心到四个顶点距离相等(到顶点和另一个底面上的顶点距离相等即可),从而求出外接球球心,然后就很容易得
几何体与外接球问题常见解法 文档格式: .pptx 文档页数: 16页 文档大小: 258.7K 文档热度: 文档分类: 幼儿/小学教育-- 教育管理 文档标签: 几何体与外接球问题常见解法 系统标
这儿是第四部分的视频资源:秒杀外接球问题(4)侧面⊥底面的几何体,高中数学如此简单 最后我们一起总结(5)一般椎体,只需要满足底面有外接圆就可