 独立同分布的指数分布的最值问题的期望
独立同分布的指数分布的最值问题的期望
800x1174 - 164KB - PNG
 指数分布的期望和方差
指数分布的期望和方差
500x375 - 14KB - JPEG

600x362 - 70KB - PNG
 正态分布的期望分布密度指数分布的期望
正态分布的期望分布密度指数分布的期望
1152x864 - 33KB - PNG
 1的指数分布,求Y的分布函数及其期望。-
1的指数分布,求Y的分布函数及其期望。-
450x410 - 18KB - JPEG
 指数分布的期望和方差.ppt
指数分布的期望和方差.ppt
1152x864 - 83KB - PNG
 判断百度指数真实度的小技巧 - 驾考宝典
判断百度指数真实度的小技巧 - 驾考宝典
680x308 - 48KB - JPEG
 指数分布随机变量的数学期望怎么求
指数分布随机变量的数学期望怎么求
600x338 - 27KB - JPEG
 概率论与数理统计,数学期望和指数分布的
概率论与数理统计,数学期望和指数分布的
352x209 - 13KB - JPEG
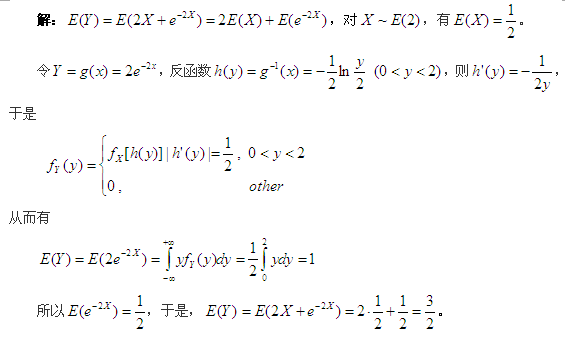 已知随机变量x服从参数为2的指数分布,求
已知随机变量x服从参数为2的指数分布,求
565x349 - 7KB - PNG
 索赔额服从指数分布的Sparre+Anderson
索赔额服从指数分布的Sparre+Anderson
800x1168 - 305KB - PNG
 对数正态分布方差证明
对数正态分布方差证明
500x375 - 15KB - JPEG
 写出指数分布的概率密度函数、累积分布
写出指数分布的概率密度函数、累积分布
507x333 - 12KB - PNG
 分布 泊松分布 指数分布 样本均值中的应用
分布 泊松分布 指数分布 样本均值中的应用
701x488 - 58KB - JPEG
 数学分布(泊松分布二项分布、正态分布、
数学分布(泊松分布二项分布、正态分布、
993x1404 - 75KB - PNG
对上述的分布函数进行求导,得到: 的概率密度函数。也就是说指数分布是可以从泊松分 顾从本篇博客开始,对广义线性模型做一个探讨,希望大家积极指出本人的问题,或参与探
[最佳答案] 首先知道EX=1/a DX=1/a^2 指数函数概率密度函数:f(x)=a*e^(ax),x>0,其中a>0为常数. f(x)=0,其他 有连续行随机变量的期望有E(X)==∫|x|*f(x)dx,(积分区间为负无穷到正无穷) 则E(X)==∫|x|*f(x)dx,(积分区间为0到正无穷),因为负无穷到0时函数值为0. EX)==∫x*f(x)dx==∫ax*e^(-ax)dx=-(xe^(-ax)+1/a*e^(-ax))|(正无穷到0)=1/a 而E(X^2)==∫x^2*f(x)dx=∫x^2*a*e^(ax)dx=-(2/a^2*e^(-ax)+2x*e^(-ax)+ax^2*e^(-ax))|(正无穷到0)=2/a^2,
[最佳答案] f(x)=λe^(-λx) E(X),对xf(x)积分,从0到正无穷。 积出的结果就是1/λ. 方差,对x^2f(x)积分。
[最佳答案] E(x²)=∫ x²λe^(-λx)dx=-x²e^(-λx)+(2/λ)∫xλe^(-λx)dx=2/λ² 说明:∫ 表示积分从0到正无穷大
[最佳答案] 首先知道EX=1/a DX=1/a^2 指数函数概率密度函数:f(x)=a*e^(ax),x>0,其中a>0为常数。 f(x)=0,其他 有连续行随机变量的期望有E(X)==∫|x|*f(x)dx,(积分区间为负无穷
[最佳答案] 是1/λ ,我查过书了,没错的
[最佳答案] 用期望和方差的定义,还有幂级数求和的知识.不好书写.lz找找概论的书,一般都会有.