不确定时变需求下单向电动共享汽车的运营管理

共享汽车作为一种新的商业模式，在提高车辆利用率和缓解交通拥堵方面取得了显著成效。然而，在现实生活中，用户的交通需求具有高度的不确定性和时变性，这对共享汽车系统的运营和管理提出了挑战。本文以应用最广泛的单程序电动共享汽车为例，对其运行管理进行建模。采用线性松弛技术对模型进行变换，并设计相应的算法加速求解，在提高求解速度的同时保证了求解质量。

1。背景介绍

1.1

共享汽车

近年来，私家车拥有量的快速增长加剧了社会和环境问题，如交通拥堵、停车位不足和温室气体排放。人们正试图探索如何减少私家车的数量，因此共享汽车的概念应运而生。以zipcar为例。共享汽车公司在运营区域内为其成员提供单向汽车预订服务(在始发站取车，在目的站还车)，并根据使用时间付费。目前，

的拼车运行模式主要分为两种:基于站点的模式，用户在指定站点上取车和返车；无站点模式，用户可以在运行区域内的任何地方返车。其中，前者可分为往返和单程，前者要求同一个车站归还汽车，后者允许汽车从其他地方归还。往返共享汽车的应用受到限制，因为它们不能满足用户的个性化需求，如modo在加拿大。单程序共享汽车能够满足客户的个性化需求，应用广泛，如中国的evcard和zipcar在美国。自由浮动共享汽车给用户带来了更多的灵活性，但也给运营和管理带来了更大的挑战，比如美国的car2go。

1.2

随机规划

共享汽车问题的主要操作挑战之一是客户需求的高度不确定性，但研究发现这种需求随时间而变化例如，用户经常集中精力在上午从郊区到城市，下午返回，这意味着交通需求的时空特征，并为后续规划提供优化空间。

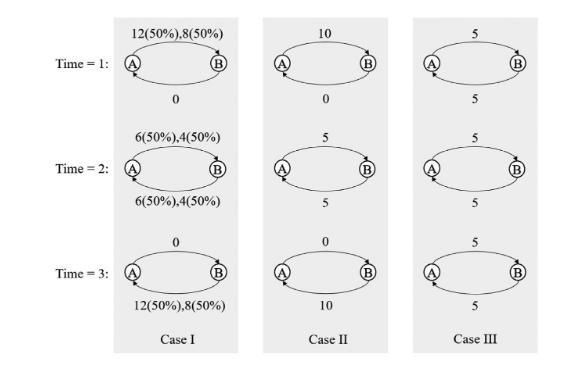
图1.1交通需求类型

将一天分为早、中、晚三个时段，各时段甲、乙站间的交通需求如图1.1所示如果忽略交通需求的不确定性和时变特性，则得到固定需求情况ⅲⅲ，因此两个站点各需要设置10个充电桩和停车位。如果添加时变特征，则获得变化的需求情况ⅱii，因此a站点需要15个停车位，b站点需要5个停车位。如果增加随机特征，则得到需求情况ⅰI，此时a站点只需设置16个停车位可以发现，与固定需求相比，具有时变和随机特性的交通需求为规划提供了优化空间。

2。型号编制

3。模型解

本文的模型是一个基于情景的多阶段问题(SMSP)，也是一个多阶段非线性整数随机规划由于维数灾难、整数变量决策和多阶段非线性的特点，直接求解这些问题非常耗时，并且需要巨大的计算资源。因此，发展了一系列线性松弛算法来减少求解时间。首先，通过放松非预期约束来应用拉格朗日松弛法，并发展投影次梯度法来解决相应的拉格朗日对偶问题。然后，发现整数变量仅在初始阶段进行决策，而后续k阶段的子问题决策仅包含连续变量，因此将其线性化为多阶段线性随机规划解。

3.1

线性化重构

3.2

线性松弛

约束(15)，车队规模变量和日常运营决策变量都是非负整数，但当问题规模较大时求解太困难，变量约束可以放宽为连续变量

这样，问题是有0-1个变量和非负连续变量当最优决策变量的值较大时，松弛解可以近似为最优解，当需求较小时，需要验证近似(感兴趣的学生可以参考参考文献1的第5.1节)

3.3

拉格朗日松弛

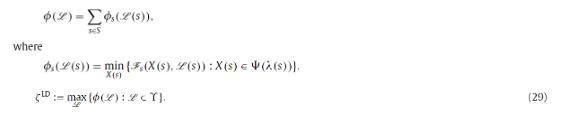
3.4

投影次梯度法

-13本节算法的伪码可以得到:

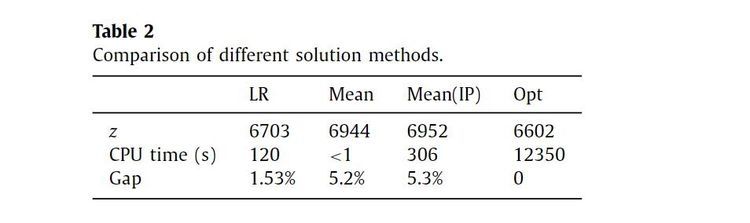
4。数值实验

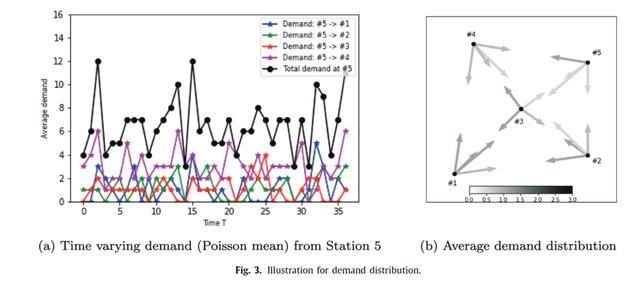
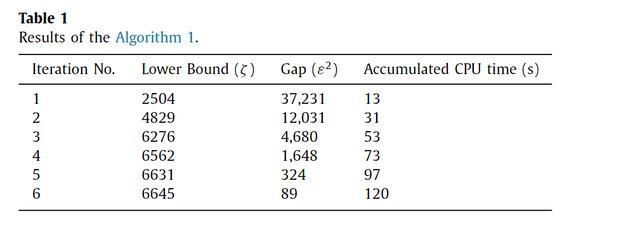
5。总结和展望

电动共享汽车系统的部署和运行，尤其是单程序共享汽车系统，是一项极具挑战性的任务，因为该系统需要处理一个具有不确定时空要求的巨大动态问题本文通过建立多阶段随机规划来描述这一复杂的决策过程，并用蒙特卡罗抽样技术来求解。同时，为了克服维数过大的问题，提出了一种基于拉格朗日松弛和SDDP算法的加速技术。对比结果表明，该算法的求解在计算时间和求解质量方面表现良好。

然而，由于随机规划问题的复杂性，解决大规模问题仍然非常困难。感兴趣的老板可以研究相关问题的加速算法。另外，本文模型的交通需求与站点位置无关。如果需求被认为受站点位置、电价和定价方案的影响，则可以得出一些有趣的结论。

因为我对随机规划的研究比较肤浅，如果有任何误解或遗漏，请讨论并指出想了解更多关于共享汽车的学生可以参考参考资料。