如何证明√2是非理性的？大学学位可能是不可能的，但完成初中学位就足够了！

，像希腊神话中的许多英雄一样，哲学家希帕索斯受到众神的致命惩罚，但是他犯了什么罪呢？希帕索斯的罪过是他发现无理数的数学证明！

希帕索斯属于一个叫做“毕达哥拉斯数学家”的团体。他们对数学怀有宗教崇敬。他们的座右铭是“一切都是数学”，数字是宇宙的基石。

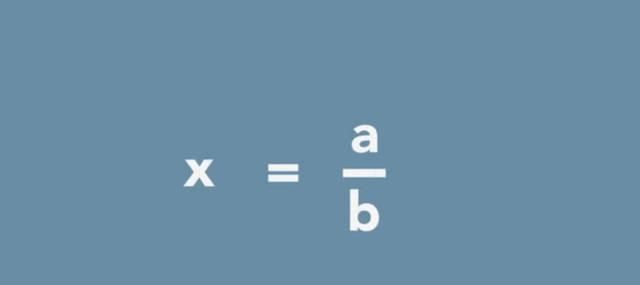
其中一个信念是，从宇宙学、形而上学和音乐中了解道德的一切事物都遵循同样的规则，这就是所谓的数的比率因此，任何数字都可以按比例书写。例如，

，5等于5/1，0.5等于1/2即使是无限循环小数，如0.3333(无限循环)，也可以精确地表示为1/3！所有这些，我们现在称之为有理数。

，但是hippasus发现一个数字违反了这个和谐的规则。它不应该存在，例如π和√2

的问题是从一个非常简单的图开始的，一个有一个边长单位的正方形。根据毕达哥拉斯定理，正方形的对角线长度是√2。但是经过努力之后，希帕索斯不能把它表示成两个整数的比值，但是他没有因此放弃，而是决心证明这是不可能的。

首先，希帕索斯假设毕达哥拉斯的世界观是正确的，也就是说，他可以用两个整数的比值来表示√2。他用P和Q来表示这两个假设的数量。假设这个比率已经被同意为最简单的形式，在P和q之间没有公约数

为了证明√2不是有理数，希帕苏斯只需要证明p/q不存在。因此，他将方程两边的Q相乘，然后将两边平方，得到这样一个方程:2Q = P

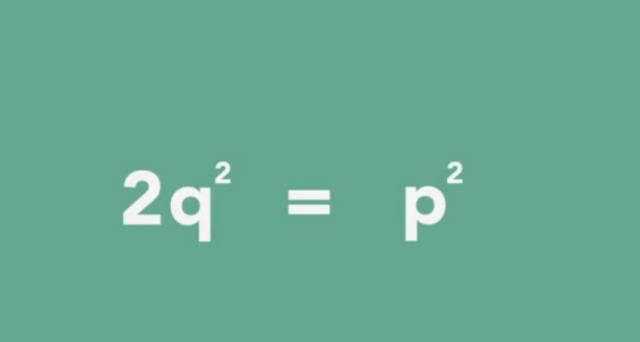
任何一个数乘以2都会得到一个偶数，所以P的平方只能是一个偶数如果p是奇数，那么p的平方不能是偶数，因为奇数的平方总是奇数，所以p是偶数，所以p可以写成2a(其中a是整数)我们把2a代入方程并简化，得到这个方程:q = 2a

，2倍任何整数都会得到一个偶数，所以既然q必须是偶数，那么q也必须是偶数，所以p和q是偶数！

，但如果是这种情况，它们有一个公约数:2，这与最初的假设相矛盾(p和q没有任何公约数)这就是希帕索斯如何证明这样一个比率不存在！这叫做反证但是根据传说，众神不喜欢被认为是矛盾的。

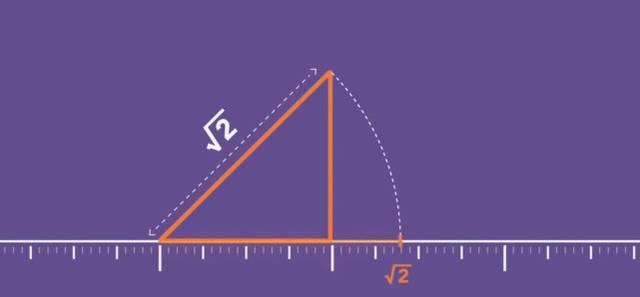
虽然我们不能用整数比的形式来表示这些无理数，但我们可以在数轴上画出一些无理数，例如√2。我们需要做的是画一个两边各有一个长度单位的直角三角形，斜边的长度是√2，它可以延伸到数轴！

这里的关键是小数和比率只是数学表达式，而√2只是两边都是1的直角三角形的斜边！

同样，π，一个著名的无理数，总是正好等于它所代表的圆周率，即圆的周长与其直径之比。它的近似值约为22/7，或355/113，但它永远不能完全等于π我们永远不会知道希帕索斯的最终结果，但我们知道他的发现带来了数学革命。所以不管传说是什么，不要害怕探索所谓的不可能！