零信任交易的POD-极小协议

摘要:zkPoD原理解释系列

作者:郭宇

本文面向具有一定密码学基础或对密码学感兴趣的读者虽然本文中有许多数学公式，但它们相对简单易懂。

简介:什么是zkPoD？

zkPoD实现了分散的“零知识有条件支付”，支持国标数据的零信任公平交易关于“零知识有条件支付”的概念，请参见概述文章“零知识证明和形式验证实现无中介无信任的公平贸易”区块链ZkPoD是实现ZKCP目标的全新方案。目前，zkPoD已经支持国标数据、低TPS公共链和高TPS联盟链。支持具有丰富类型和结构的二进制数据和表格数据。与传统的“可信第三方”相比，zkPoD利用区块链作为“可信第三方”来实现“零信任公平交易”

zkPoD也是实现数据和价值双向流动的底层基本协议。有关开放源代码和更多文档，请参见:https://github.com/sec-bit/zkpod-nod

防泄露协议

PoD是实现zkPoD系统的核心协议PoD协议利用区块链的智能契约实现了“数据”和“令牌”的原子交换，保证了买卖双方的公平。PoD不像ZKCP那样采用单一的zkSNARK方案来实现原子交换，而是使用经典的密码方案，如PedersenCommitment和SchnorrProtocol。通过这种方式，PoD可以变得更加高效和易于扩展。PoD协议也将使用形式证明来建立一个坚实的“信任基础”。

本文介绍了一个非常简单的PoD协议——PoD-TINY。该协议简化了许多细节，并且不实用，但是它可以帮助读者快速理解POD的原理和挑战。

假设我是卖家，你需要从我这里购买一个数据文件。本协议的一般流程是:

步骤1:我加密“数据”并将其传递给你步骤2:你将“令牌”交给区块链的“智能合同”步骤3:我用“密钥”交换“智能合同”中的“令牌”。然后，您可以从智能合同中读取“密钥”来解密“数据”。很简单吗？聪明，你现在高度怀疑这个过程是否有任何问题。

公平交易中的关键问题

关键问题:您收到的加密数据确实是您想要的数据的关键问题:在您收到加密数据后，如何在不付费的情况下运行？我向智能契约展示的密钥必须是真正的密钥，否则我无法获得令牌密钥问题:在我展示真正的密钥之后，我必须能够获得令牌。然后，我们将破茧而出，讨论PoD-Tiny如何巧妙地解决这些问题。

锁定数据的特性:授权码

对于关键问题，我们需要一个定位点。你想要什么数据为了简单起见，让我们假设我们之前已经就数据文件的唯一标签或特征达成一致。那么你购买的数据需要一个接一个地对应这个标签。

一般来说，人们喜欢用哈希来标记字符串的特征，例如，计算

h=MD5来解决这个问题的核心方法是“零知识证明”如果买方在收到加密数据后不能分析任何额外的信息，那么卖方的利益不会受到损害，关键问题将得到解决。简而言之，如果加密数据一无所知，买家就不会害怕拿走加密数据，带着钱逃跑。所谓的“零知识”可以用这样一种流行的方式来理解:买家得到加密数据后，就像得到一堆没有任何信息的随机数。如何实现零知识？PoD-Tiny采用了经典Schnorr协议的思想。

关键问题:收到加密数据后，如何不付费运行？回想一下关键问题:

通过同态，买家可以在数据加密的情况下验证数据是否满足某些条件

summary:

，通过上面的公式，您还可以知道一条关键消息:该密钥是一个与k相关联的值虽然此时你根本不知道m和k键这些信息也是解决关键问题的关键。

E*G？=K+A

其余的很简单。在PoD协议中，我们可以选择一个随机数K作为一次性密钥来加密M，并计算E = K+Me是加密数据我也可以给你发K=k*G，所以你手里有三样东西，a，K和e您可以使用下面的公式来“同态”验证加密的e确实是数据m的密文:

注意:这里的加法是模加法，a+b是a+bmodp的缩写为了易读，所有随后的加、减、乘和除都被认为是有限域上的运算。

验证m1？=m2+m3你可以发现，虽然吃瓜的人知道A1，但他不能反过来计算m1然而，他仍然知道m1等于另外两个数的和，尽管他不知道这三个数的具体值。

我们可以计算A1吗？=A2+A3

A1=m1*G，A2=m2*G，A3=m3*G，

他们的验证者分别计算如下:

“验证信息”他们为什么使用这种“承诺”形式而不是众所周知的哈希运算这是因为“承诺”具有加法同态所谓同态性质可以理解如下:明文数据的一些运算可以同态映射到密文运算假设有三个数据明文，m1、m2和m3，其中m1=m2+m3

“认证信息”认证器可以向所有人公开，我们不必担心泄露原始数据信息。这是因为很难从a计算m。这种逆运算是有限域“对数”运算如果有限域相对较大，这种对数运算非常非常困难，这通常被称为“离散对数问题”假设。抛开这些理论细节，我们只需要知道Authenticator可以把它给任何人，而不用担心m会被反向破解。

承诺也称为提交，它可以实现与数据的一对一对应，同时可以隐藏数据的价值。在zkPoD系统中，这里有一个被称为“认证信息”的认证器。这里G是椭圆曲线循环群的生成元

A=m*G

我们通过以下操作为此数据生成一个“承诺”

让我们看看字符串“你好，zkPoD！”总共有12个字节，即96位。所以我们可以把这12个字节转换成一个有限域上的整数。这样，我们可以将这个字符串编码成一个整数。让我们用一个符号来表示这个整数，假设m。

插入科普:schnoor协议和“零知识”

schnoor协议是非常经典的教学书籍示例。我会带你在这里快速浏览。施诺尔协议的用途之一是进行身份认证。这是一个双方安全协议。一个“证明者”爱丽丝向另一个“验证者”鲍勃证明她有一个对应于公钥的私钥。

首先爱丽丝生成一对“公钥和私钥”。鲍勃然后持有爱丽丝的公钥主键当爱丽丝想向鲍勃证明她的身份时，他们将通过“三步交互协议”来完成证明:证明爱丽丝拥有私钥sk如果鲍勃接受这个证书，他会认为爱丽丝是在相反的证书中拥有私钥的人。下面是该协议的简要描述:

sk=a，pk=a*G

公共输入:PK = a * G

爱丽丝私人输入:sk=a

第一步:爱丽丝选择一个随机数R，并将R的“承诺”R=r*G发送给鲍勃

第二步:鲍勃发回一个随机数c，作为挑战号

的第三步，爱丽丝计算=R+c*PK=r*G+c*a*G

此Schnorr协议有三个属性:

完整性可靠性特殊不确定性对诚实验证者来说是零知识，其第三个属性是“零知识”，这确保了Bob在协议交互过程中不会以任何方式获得关于私钥的任何信息。

注:严格来说，施诺尔协议不是“全ZK”，而只是“高兹克”，这是一个相对较弱的零知识属性。然而，我们暂时不必担心这个。施诺尔协议可以通过一些技术升级到“全ZK”。

PoD-Tiny:一个简单的PoD协议

如果你可能还记得施诺尔协议的细节，那么让我给你看一个叫做PoD-Tiny的协议

协议描述:假设爱丽丝有一个数据明文m，那么鲍勃有这个数据的认证者，这里还有一个“不可信的第三方”。我们暂时叫她朱莉娅吧请记住:她是一个聪明的合同

协议:

开场前道具:m，a，G，随机数生成器随机

角色:

爱丽丝:有数据m，一次性密钥k

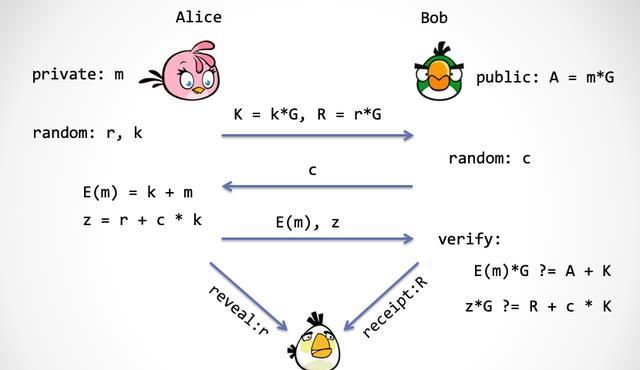
步骤:

第一步:爱丽丝生成随机数，r