自然对数_自然对数函数

马平:6亿美元,看不到另一个地球也很值

514x660 - 23KB - JPEG

数学--自然对数表

606x527 - 153KB - JPEG

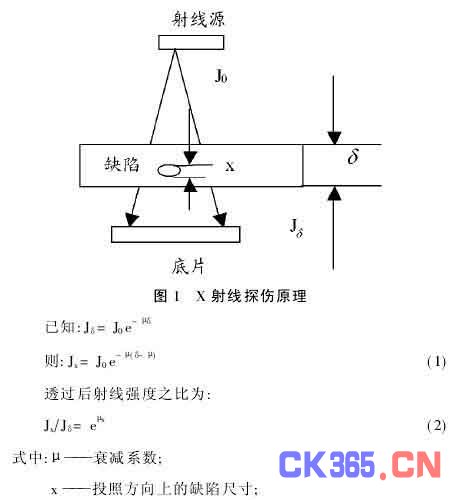
X射线检测钢丝绳成像系统设计

456x500 - 19KB - JPEG

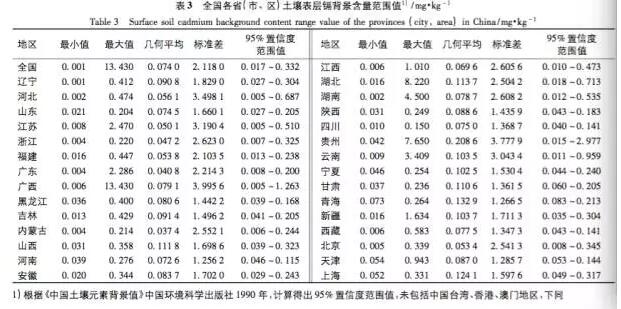
土壤重金属镉标准值差异比较研究与建议_绿色

621x309 - 46KB - JPEG

没看懂对数函数的换底公式和自然对数-+已解决

500x375 - 13KB - JPEG

圆周率与自然对数

640x355 - 78KB - JPEG

在excel中使用自然对数函数LN的图文教程

861x575 - 174KB - PNG

自然对数的底数e为2.718281828的秘密-搜狐教

600x450 - 137KB - PNG

设(e为自然对数

507x201 - 14KB - JPEG

自然对数回归模型怎么做? - 线性回归 - 知乎

583x251 - 14KB - PNG

关于自然对数底e的推导过程中的一些问题

600x200 - 17KB - PNG

我对你的思念就像循环小数

305x240 - 14KB - JPEG

两种计算自然对数的算法比较_「电脑玩物」中

384x551 - 216KB - PNG

[自然对数e的由来]自然对数底数e的由来.doc

993x1404 - 73KB - PNG

自然对数

629x1345 - 32KB - PNG

简介：通常以logaX作为对数的表达法，对数的值通常为底数a的幂，X为a的N次幂的值。自然对数一般为lnX，就是以e

自然对数底也叫工程系数,在高中阶段非常重要,但是容易被同学们忘记,通过这个故事,也许对大家记忆这个无理数有所帮助工具/原料无理数e圆周率

好问题,让我尝试不用公式,用跨越7000年人类文明的方式,来解读e的自然之美,争取有中学基础的人就能看懂。 e有时被称为自然常数(Natural constant),是一个约等于2.71828182845904523536……的无理数。 以e为底的对数称为自然对数(Natural logarithm),数学中使用自然(Natural)这个词的还有自然数(Natural number)。这里的“自然”并不是现代人所习惯的“大自然”,而是有点儿“天然存在,非人为”的意思。就像我们把食品分为天然食品和加工食品,天然食品就是未经人为处理的食品。 但这样解读“自然”这个词太浅薄了!为了还原全貌,必须穿越到2500多年前的古希腊时代。 (你也知道,穿越剧都很长(>﹏<),不喜欢长篇大论的,可直接跳到后面看结论。) “自然”的发明 我们知道,人类历史上曾出现过很多辉煌的文明,例如大家熟知的四大文明:古巴比伦、古埃及、古印度河以及古代中国。 但是要说谁对现代文明的影响最大?对不起,四大文明谁都排不上!真正对现代文明影响最大的是古希腊文明,特别是古希腊的哲学、科学思想,是整个现代文明的源头和

e是自然对数的底数,是一个无限不循环小数,其值是2.71828……,是这样定义的: 当n->∞时,(1+1/n)^n的极限。 注:x^y表示x的y次方。 随着n的增大,底数越来越接近1,而指数趋向无穷大,那结果到底是趋向于1还是无穷大呢?其实,是趋向于2.71828……,不信你用计算器计算一下,分别取n=1,10,100,1000。但是由于一般计算器只能显示10位左右的数字,所以再多就看不出来了。 e在科学技术中用得非常多,一般不使用以10为底数的对数。以e为底数,许多式子都能得到简化,用它是最“自然”的,所以叫“自然对数”。 我们都知道复利计息是怎么回事,就是利息也可以并进本金再生利息。但是本利和的多寡,要看计息周期而定,以一年来说,可以一年只计息一次,也可以每半年计息一次,或者一季一次,一月一次,甚至一天一次;当然计息周期愈短,本利和就会愈高。有人因此而好奇,如果计息周期无限制地缩短,比如说每分钟计息一次,甚至每秒,或者每一瞬间(理论上来说),会发生什么状况?本利和会无限制地加大吗?答案是不会,它的值会稳定下来,趋近於一极限值,而e这个数就现身在该极限值当中(当然那时候还没给

这正是 Euler名字的第一个字母,后来人们确定用 e来作为自然对数的底,以此来纪念欧拉. 事实上 ,用 e作为自然对数的底的另一个原因是它和指数有

特别地,以10为底的对数叫常用对数,记作log10N,简记为lgN;以无理数e(e=2.718 28…)为底的对数叫做自然对数,记作logeN,简记为lnN. 2对数式与指

自然常数 确实是一个奇妙的数字,这里的 并不仅仅是一个字母,它还代表数学中的一个无理常数,约等于 。 但为啥一个无理数却被人们称之为“自然常数”? 说到 ,我

课程简介:这一部分主要介绍了对数的表示和求解(包含自然对数的内容)。主要内容有:对数介绍,对数性质,对数的和与乘积,对数方程,对数性质的证明,自然对数以及对数的图像等