中线长定理_三角形中线长定理

中线长定理_互动百科

300x225 - 7KB - JPEG

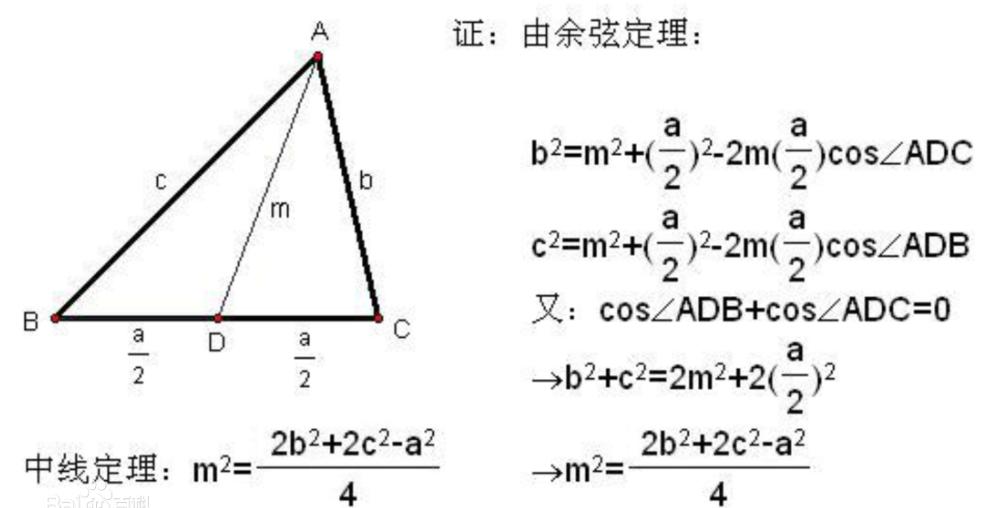
中线定理

1007x508 - 41KB - JPEG

中线长定理+-+搜搜百科

200x150 - 5KB - JPEG

学 初高中衔接教程 第五讲 几何中的著名定理练

993x1404 - 56KB - PNG

高中数学衔接教程:第五讲 几何中的著名定理.d

993x1404 - 57KB - PNG

梯形的重心定理及中线长公式

278x392 - 40KB - JPEG

中线向量定理和非中线向量定理分别是什么,_高

550x282 - 10KB - JPEG

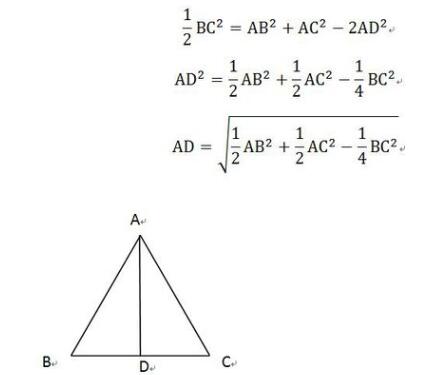
三角形中线定理计算方法

436x375 - 9KB - JPEG

21平行四边形定理与三角形中线长公式

448x252 - 26KB - JPEG

看不懂这个式子,不要和我说什么中线定理

550x284 - 13KB - JPEG

三角形中线定理

231x156 - 6KB - JPEG

直角三角形斜边中线定理

300x187 - 4KB - JPEG

北师大版数学九下3.7《切线长定理》word同步

993x1404 - 89KB - PNG

中线定理_互动百科

220x220 - 7KB - PNG

所以底边高也是底边的中线根据勾股定理

400x300 - 4KB - JPEG

简介：中线定理（pappus定理），又称阿波罗尼奥斯定理，是欧氏几何的定理，表述三角形三边和中线长度关系。 三角

三角形中线长定理的趣用 中国学术期刊网|2013-05-28 |举报 中国学术期刊网中国规模最大的中文学术期刊荐稿网络|总评分0.0|文档量0|浏览量0 专业文档 专业文档是百度文库

任意三角形ABC中,D是底边BC上一点,连结AD,则有:AB^2*CD+AC^2*BD=(AD^2+BD*DC)*BC 也可以有另一种表达形式:设BD=u,DC=v,则有:AD^2=(b^2×u+c^2×v)/a-uv .当D

结论最后应该是"加上3个DE的平方"。 设BC中点为M,在△ADE,△MDE中应用余弦定理,得 AD^2=AE^2+DE^2-2*AE*DE*cos∠AED, MD^2=ME^2+DE^2-2*ME*DE*cos∠MED, 因为AE=2ME,cos∠AED=-cos∠MED,所以 AD^2+2MD^2=AE^2+2ME^2+3DE^2.(*) DM,EM分别是△DBC,△EBC的中线, 2DM^2=DB^2+DC^2-BC^2/2, 2EM^2=EB^2+EC^2-BC^2/2, 代入(*)式,即得 DA^2+DB^2+DC^2=EA^2+EB^2+EC^2+3DE^2. 用解析几何的方法也不难证明。还可以用物理中转动惯量的有关定理证明。 AE=2ME,重心把中线分成2:1的两段。 cos∠AED=-cos∠MED,因为∠AED+∠MED=180°。 "DM,EM分别是△DBC,△EBC的中线, 2DM^2=DB^2+DC^2-BC^2/2, " 这个一般叫中线长公式,该学过吧。

方法一:直接应用三角形中线长计算公式。 ∵m=(1/2)√(2AB^2+2AC^2-BC^2) ∴4m^2=2(AB^2+AC^2)-64, ∴2m^2=AB^2+AC^2-32, ∴2m^2=(AB+AC)^2-2AB×AC-32, ∴2m^2=100-32-2AB×AC=68-2AB×AC。 在△ABC中,显然有:AB、AC都是正数,∴AB+AC≧2√(AB×AC),∴100≧4AB×AC, ∴-2AB×AC≧-50。 ∴2m^2=68-2AB×AC≧68-50=18, ∴m^2≧9。 ∵m>0,∴m≧3。 ∴m的最小值为3。 方法二: ∵BC=8,又BD=CD,∴BD=CD=4。 由斯特瓦德定理,有:AB^2×CD+AC^2×BD-AD^2×BC=BC×BD×CD, ∴4AB^2+4AC^2-8m^2=8×4×4,∴2m^2=AB^2+AC^2-32。 同方法一,得:m的最小值为3。

中线长定理:三角形一条中线的两侧所对边的平方和等于底边一半的平方与该边中线的平方和的2倍 已知:AD是三角形ABC的中线 求证:AB^2+AC^2=2(1/2BD)^2+2AD^2 证明:过

【摘要】:正中线长定理在初中几何中很少触及,但运用它来解决某些问题,常有奇效.本刊在2002年第3期载有《用中线长定理解题》,下面首先给出证明. 支持CAJ、PDF文件格式

中线长定理的证明在三角形ABC中的任一一点中就是证明斯特沃特定理。在三角形ABC中的任一一点D,E是重心(就是三条中线的交点)。DA的平方加上DB的平方加上DC的平方

【摘要】:正贵刊2002年第9期《中线长定理的证明与妙用》一文,给出了中线长定理证明过程,并巧妙地应用于一道作图题.其实,平面几何中带有中线的问题,一般都可用中线长定

求中线长定理证明三角形ABC中,若D是AB的中点,则AD^2+BD^2+2CD^2=BC^2+AC^2这个定理如何证明?最好告诉我与椭圆有何关系. 下载作业帮 扫二维码下载作业帮 4亿+用