数值分析中的有效数字_数值分析有效数字

数值行分析1-误差及有效数字.ppt

1152x864 - 1065KB - PNG

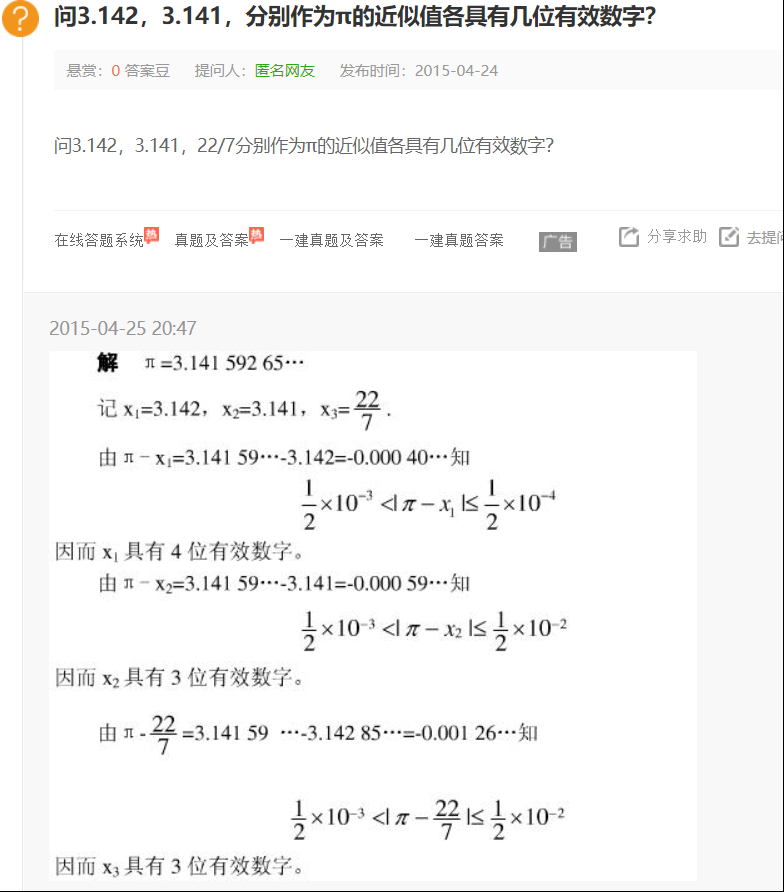
怎样理解数值分析中对有效数字的定义以及为什

784x892 - 107KB - JPEG

怎样理解数值分析中对有效数字的定义以及为什

941x757 - 123KB - JPEG

怎样理解数值分析中对有效数字的定义以及为什

1104x432 - 35KB - JPEG

怎样理解数值分析中对有效数字的定义以及为什

299x286 - 7KB - JPEG

数值分析1误差及有效数字摘要.ppt

1152x864 - 1054KB - PNG

第一章 有效数字和误差分析.ppt

1152x864 - 175KB - PNG

第一章 有效数字和误差分析#.ppt

141x200 - 8KB - JPEG

WOW7.1.5暗牧橙装推荐搭配及饰品分析:塞咪

459x206 - 30KB - JPEG

7.1.5暗牧橙装推荐搭配及饰品分析:塞咪咪也很

302x319 - 28KB - JPEG

解析安卓大屏广告机怎样的互动形式最有效 -电

1200x800 - 38KB - JPEG

于msc.dytran的人-椅系统冲击动力学仿真分析(

625x254 - 19KB - JPEG

②该同学根据实验数据.利用计算机作出t2-l图线

170x242 - 9KB - PNG

如何按四舍五入法将数值保留n位有效数字

1000x562 - 43KB - JPEG

环境监测中如何进行数值修约及有效数字的取舍

1080x581 - 133KB - JPEG

原 数值分析中对有效数字的定义 zjpp2580369 阅读数:1267 2018-11-11 设数x是数x的 并且从x左起第一个非零数字到该数位共有n位,则称这n个数字为x的有效数字,也称用x近

即应取4位有效数字,近似值的误差不超过0.1%.内容来自淘豆网www.taodocs.com转载请 2015年第5期分析培训-有效数字和数值的修约. 数值分析1-误差及有效数字-课件PPT(演

您可以和千万网友分享自己手中的文档,全文阅读其他用户的文档,同时,也可以利用分享文档获取的积分下载文档 有效数字的运算规则 河 海 大 学 数 值 分 析 有 效 数 字 82645

数值分析:研究各类数学问题求解的数值计算及相关理论分析。随着计算机的产生和发展 且该位直到的第一个非零数字共有n位,则有n位有效数字。 具体计算:对,从左往右数,从第

不是楼上说的那样的,数值分析中有效数字需要根据公式判断,有点麻烦,建议楼主找本书看看就会了 追问: 我有书,可是看不懂 追答: 你一步一步对照着做,先化成标准形式,再求差

数值分析里的有效数字定义如下: 如果近似值x的误差限是其某一位上的半个单位,且该位 有效数字。 比如: 0.0109,前面两个0不是有效数字,后面的109均为有效数字(注意,中间的

数值分析里的有效数字定义如下: 如果近似值x的误差限是其某一位上的半个单位,且该位直到x的第1位非零数字一共n位,则称近似值x有n位有效数字。 比如: 0.0109,前面两个0不是有效数字,后面的109均为有效数字(注意,中间的0也算); 3.109*10^5(3.109乘以10的5次方)中,3 1 0 9均为有效数字,后面的10的5次方不是有效数字。; 5.2*10^6,只有5和2是有效数字; 0.0230,前面的两个0不是有效数字,后面的230均为有效数字(后面的0也算)。

简介：有效数字 :具体地说，是指在分析工作中实际能够测量到的数字。能够测量到的是包括最后一位估计的，不确定的数

这个概念好像和中学学的好像就是不太一样,我刚看到这个概念的时候也比较懵。其实现在还是懵的。就大概说一下我的想法你参考参考,不一定对。中学那个后面所有的数字都要算作有效数字的。基于标尺测量的话,是几个准确位加一个估计位。数值分析里有效数字计算是要求全部精确位的,我理解为从第一个非零位开始,到最后一个精确位结束。这个和算误差就可以直接联系起来。这个估计位可能就是那个所谓的半个单位(0.5*10^n)的来历。你想,标尺读数估读最后一位的时候,虽然该位不准确,但在0.5前后的趋势是不会错的,也就是长度末点占了一格的一多半还是一小半是无疑的,末点仅仅超出标度一点点你可能会估读成1,2,3,4,但是绝对不允许读成7、8。因此这一位虽然不精确,但误差绝对超不过5,也就是说误差限不超过前面精确位的一半(也就是最小格的一半)。这样理解的话,“最后一位精确位”和“误差限半个单位”就有联系了。那之后计算有效数字也简单了,先算误差是小于哪一位的一半,那么那一位就是最后一位精确位。然后从前往后还是从后往前数数有几位都可以。

数值分析:误差及有效数字 下载积分:200 /* Error */§1 误差的背景介绍 /* Introduction */1.来源与分类 /* Source & Classification */ 从实际问题中抽象出数学模型——模型误差 /* M